sparse tables

I guess I am a fan of tables. Also I thought this will be a quick write up since my last blog had suggestions to convert it into a gitbook. (It was that huge) Although I hope you like this one, it won't take much of your time.

Sparse Tables, it's probably a niche data structure with a great time complexity when answering range queries on static arrays.

Motivation

Alright! Let's talk about the type of situation where you might want to use sparse tables. As I said, it's all about doing efficient range queries on static arrays. So, a typical use case is when you're dealing with say an integer array that has immutable data i.e. does not change over the course of time.

Some common types of range queries that you often want to know are things like finding the minimum value in a certain range, may be finding the sum, product, gcd, etc. For a significant amount of queries, you would definitely not want to take a lot of time (i.e. brute force) in processing the solution.

Intuition

I'd like to give you a brief intuition on how a sparse table works at a high level without getting into too many details.

So, if you think about any positive integer, you know that it can easily be represented as the sum of powers of 2, given by it's binary representation. For example:

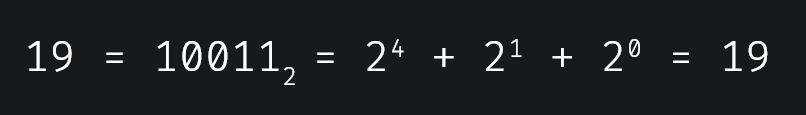
Similary we can break down an interval l, r with a left and a right end point into ranges of lengths that are powers of 2. For example:

Here, 5, 17 is broken down into three ranges of length 8, 4, and 1. Now imagine if we could precompute the range query answer (i.e min, max, sum ...) for all these intervals and combine them. Well that's the direction we are headed in so we can answer numerous types of range queries with a sparse table. However all range query functions need to meet certain prerequisites in order to be compatible with the types of aggregation and combination operations that we want to do while building the sparse table and also while performing range queries.

Prerequisites

The first is that the binary range combination function is associative which means that the order in which operations are performed, does not matter.

More formally:

f(x, y) is associative if:
f(a, f(b, c)) = f(f(a, b), c) for all a, b, c

Operations like addition, multiplication are associative, but functions like subtraction and exponentiation are not. Here's a counterexample proving subtraction is not associative:

Let f(a, b) = a - b
f(1, f(2, 3)) = f(1, 2 - 3) = f(1, -1) = 2
f(f(1, 2), 3) = f(1 - 2, 3) = f(-1, 3) = -4
∴ f is not associative

If your range combination function is associative, then you can do range queries on a sparse table in logarithmic O(log₂(n)) time.

Range Combination Function

Logarithmic time range queries are really good, however we can do better. When the range query combination function is overlap friendly, then range queries on a sparse table can be answered is O(1). And by overlap friendly, means a function yields the same answer regardless of whether it is combining ranges which overlap or those that do not.

We say a binary function f(x, y) is overlap friendly if:

f(f(a, b), f(b, c)) = f(a, f(b, c)) for all valid a, b, c

Well if it's still not clear let's see an example:

Consider this array and a summation function f(x, y) which just adds x and y. Unfortunately, this is not overlap friendly and I can easily show you why. Here I have already computed the sum of three arbitrary ranges denoted r1, r2 and r3. What we're trying to test is whether our function is agnostic to the middle interval r2. 7, 3, 24

f(f(r1, r2), f(r2, r3)) = f(f(1, 3), f(3, 24)) = f(4, 27) = 31
and
f(r1, f(r2, r3)) = f(7, f(3, 24)) = f(7, 27) = 34
∴ f is not overlap friendly

What ends up happening in the case specifically is that the summation function double counts the middle interval twice.

Q. Which of these are overlap friendly functions?

f(a, b) = 1 * b
f(a, b) = a * b
f(a, b) = min(a, b)
f(a, b) = max(a, b)
f(a, b) = a + b
f(a, b) = a - b
f(a, b) = (a * b) / a , a != 0
f(a, b) = gcd(a, b)

f(a, b) = 1 * b
f(a, b) = min(a, b)
f(a, b) = max(a, b)
f(a, b) = gcd(a, b)

Table Construction

The central idea behind a sparse table is to pre compute the range query answers for all intervals of size 2^x to efficiently answer range queries between l, r. The main downside to this approach is that you need O(Nlog(N)) memory to store all the intervals but in the end you end up reaping the benefits with fast queries. So that's a tradeoff you need to make to get started.

Let N be size of the input values array, and let 2^P be the largest power of 2 that fits in the length of the values array.

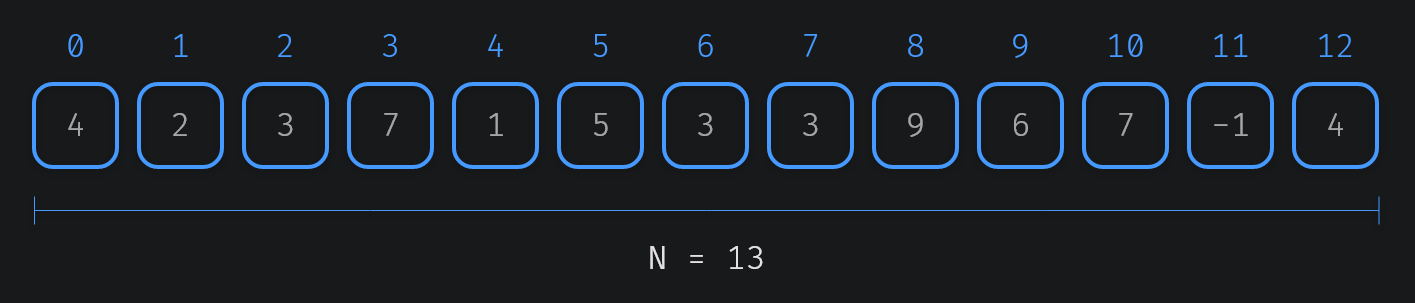
P = floor(log2(N)) = floor(log2(13)) = 3

So now we have our two required variables N and P. We begin by initializing a table with P+1 rows and N columns. Next up we can fill the first row with the input values.

Each cell (i, j) represents the answer for the range [j, j + 2ⁱ) in the original array. ¹

For example, cell (2, 5) represents the answer for the range [5, 9). If we're building a min sparse table then the (2, 5) cell would have a value of 3. And if the table is a sum sparse table, it would have 20.

It'll obviously vary depending on what you're trying to accomplish with the sparse table. Try clicking on cell (3, 2), you'll se it represents the answer for range [2, 10), 10 non inclusive.

But if you'll notice non clickable cells (grey) like cell (2, 10) which represents [10, 14). This interval reaches outside the bounds of sparse table. Well, we don't need to consider partial ranges, so we can actually simply ignore this cell and all other with invalid intervals.

Now that we understand what each cell represents, let's build a sparse table to support minimum range queries. So we'll first a need a range combination function to combine cells together:

f(x, y) = min(x, y)

The way we'll build the table is by reusing already computed range values of previous cells. We know that the current cell (i, j) represents the range [j, j + 2ⁱ ) which always has even length. This range can be broken into two sub intervals (which we will have already computed).

Suppose, we want to know the value of the pink cell (3, 2). To compute its value we'll take the minimum of both the orange cells, which represent intervals of length 4, which combined together cover the same range as the pink cell would. In turn the orange cells are computed from the green cells, which represent intervals of size 2. And those greens are based on blue cells. So the pink cell has the minimum value covered by all the blue cells.

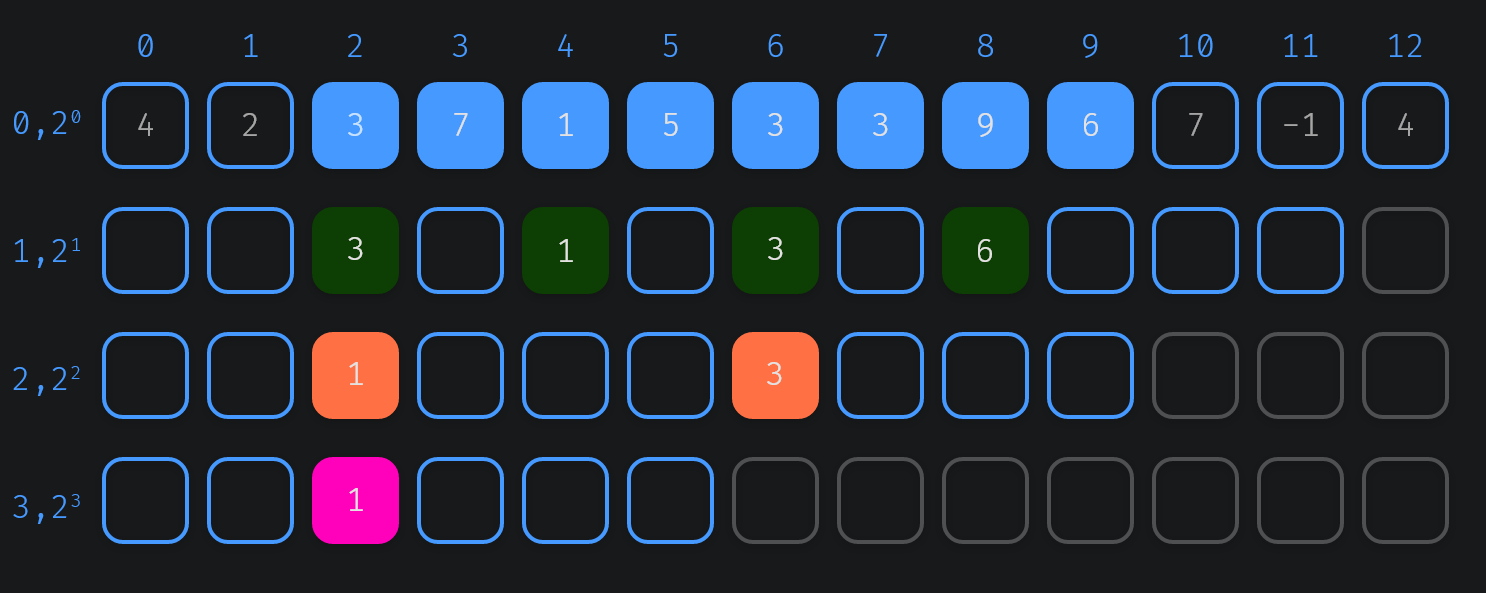
So, more specifically the range for the cell (i, j) can be split into a left interval [j, j + 2^i-1 ) and a right interval [j + 2^i-1, j + 2ⁱ ) whose values would correspond to the cells (i-1, j) and (i-1, j + 2^i-1 )

Now we can finish filling the sparse table by combining values from the previous rows(dynamic programming).

dp[i][j] = f(dp[i-1][j], dp[i-1][j+pow(2, i-1)])
         = min(dp[i-1][j], dp[i-1][j+pow(2, i-1)])

Great! We're finished building the minimum sparse table.

Range Queries

Well, in the table we have already precomputed the answer for all intervals of length 2^x . Let k be the largest power of two that fits in the length of the range between l, r.

Knowing k we can easily do a lookup in the table to find the minimum in between the ranges l, l + k (left interval) and r-k+1, r (right interval) to find the answer for l, r. The left and right intervals may overlap, but this doesn't matter (given the overlap friendly property) so long the entire range is covered.

Now suppose we want to know the minimum value between 1, 11?

len = l - r + 1 = 11 - 1 + 1 = 11
P = floor(log2(len)) = floor(3.321) = 3
k = pow(2, P) = pow(2, 3) = 8

= min(dp[P][l], dp[P][r - k + 1])
= min(dp[3][1], dp[3][4])
= min(1, -1)
= -1

Associative Function Queries

Some functions such as multiplication and summation are associative, but not overlap friendly. Luckily a sparse table can still acccomodate such functions for range queries. However, the runtime will be logarithmic instead of constant.

The alternative approach to performing a range query is a cascading query on a sparse table. You can do this by breaking the range l, r into smaller ranges of size 2 to the power x which do not overlap.

For example range between 2, 15 can be split into three intervals of length 8, 4, and 2.

[2, 10) U [10, 14) U [14, 16)

Consider the input array: 1, 2, -3, 2, 4, -1, 5

Suppose, we want to find the product of all the elements between 0, 6 using a sparse table. First we would construct a table like we did before:

Let's break it down into ranges of size of powers of 2: [0, 2²) U [4, 4 + 2¹) U [6, 6 + 2⁰)

And then we lookup the value of each interval in the table and take the product of all the intervals:

= dp[2][0] * dp[1][4] * dp[0][6]
= -12 * -4 * 5
= 240

Pseudocode

Let's see how we'll go about coding an efficient sparse table. We'll have

• N, the number of elements in the input array
• P, short for power calculated as floor(log2(N))
• log2 = ... , A quick lookup table for floor(log2(i)), 1 <= i <= N
  • size: N+1, index 0 will be unused
• dp, the sparse table with P+1 rows and N columns
• it = .. , P+1 rows and N columns
  • Index Table (IT), this will be associated with the values in the sparse table. This table is only useful when we want to query the index of the min(or max) element in the range l, r rather than the value itself. This table doesn't make sense for most other range queries like gcd or sum.

function BuildMinSparseTable(values):
  N = length(values)
  P = floor(log(N) / log(2))
  // Quick lookup table for floor(log2(i))
  log2 = [0, 0, ..., 0, 0]
  for (i = 2 ; i <=N ; ++i):
    log2[i] = log2[i/2] + 1
  // fill first row
  for (i = 0 ; i < N ; ++i):
    dp[0][i] = values[i]
    it[0][i] = i
  for (p = 1 ; p <= P ; ++p):
    for (i = 0 ; i + (1<<p) <= N  ; ++i):
      left = dp[p-1][i]
      right = dp[p-1][i + (1<<(p-1))]
      dp[p][i] = min(left, right)
      // propagate the index of smallest element
      if left <= right:
        it[p][i] = it[p-1][i]
      else:
        it[p][i] = it[p-1][i + (1 << (p-1))]
// Query the smallest element in range [l, r], O(1)
function MinQuery(l, r):
  len = r - l + 1
  p = log2[len]
  left = dp[p][l]
  right = dp[p][r - (1<<p) + 1]
  return min(left, right)
// Cascading Min Query for range [l, r], O(log2(n))
function CascadingMinQuery(l, r):
  minVal = inf
  for (p = log2[r - l + 1] ; l <= r  ; p = log2[r - l + 1]):
    minVal = min(minVal, dp[p][l])
    l += (1<<p)
  return minVal
// Returns index of min element in range [l, r]
// if multiple values index of leftmost is returned
function MinIndexQuery(l, r):
  len = r - l + 1
  p = log2[len]
  left = dp[p][l]
  right = dp[p][r - (1<<p) + 1]
  if left <= right:
    return it[p][l]
  return it[p][r - (1<<p) + 1]

C++ Implementation

You can also have a look at the C++ implementation of the above Pseudocode.

//g++  7.4.0
/*
 * Min Sparse Table Example
 *
 * @author Karn, mail@karngyan.com
*/
#include <bits/stdc++.h>
using namespace std;
class MinSparseTable {
    
    int n, P;
    vector<int> log2;
    vector<vector<int>> dp, it;
    int inf = 1e9;
    
public:
    vector<int> values;
    
    MinSparseTable(vector<int> &values) {
        n = values.size();
        P = (int) (log(n) / log(2));
        dp.resize(P+1, vector<int>(n));
        it.resize(P+1, vector<int>(n));
        
        for (int i = 0 ; i < n ; ++i) {
            dp[0][i] = values[i];
            it[0][i] = i;
        }
        
        log2.resize(n+1);
        for (int i = 2 ; i <= n ; ++i)
            log2[i] = log2[i/2] + 1;
        
        for (int p = 1 ; p <= P ; ++p) {
            for (int i = 0; i + (1<<p) <= n ; ++i) {
                int leftInterval = dp[p-1][i];
                int rightInterval = dp[p-1][i + (1 << (p-1))];
                dp[p][i] = min(leftInterval, rightInterval);
                
                if (leftInterval <= rightInterval)
                    it[p][i] = it[p-1][i];
                else
                    it[p][i] = it[p-1][i + (1 << (p-1))];
            }
        }
    }
    
    int MinQuery(int l, int r) {
        int len = r - l + 1;
        int p = log2[len];
        int left = dp[p][l];
        int right = dp[p][r - (1<<p) + 1];
        return min(left, right);
    }
    
    int CascadingMinQuery(int l, int r) {
        int minVal = inf;
        for (int p = log2[r - l + 1] ; l <= r  ; p = log2[r - l + 1]) {
            minVal = min(minVal, dp[p][l]);
            l += (1<<p);
        }
        return minVal;
    }
    int MinIndexQuery(int l,int r) {
        int len = r - l + 1;
        int p = log2[len];
        int left = dp[p][l];
        int right = dp[p][r - (1<<p) + 1];
        if (left <= right)
            return it[p][l];
        return it[p][r - (1<<p) + 1];
    }
};
int main() {
    
    vector<int> values = {1, 2, -3, 2, 4, -1, 5};
    MinSparseTable minSparseTable(values);
    
    cout << minSparseTable.MinQuery(1, 5) << endl; // -3
    cout << minSparseTable.MinIndexQuery(1, 5) << endl; // 2
    
    
    return 0;
}

That's about it! Hope you had a good time :). Do subscribe if you're interested to get notified for further posts.